Improved Denoising Diffusion Probabilistic Models : arxiv
Improved Denoising Diffusion Probabilistic Models
Denoising diffusion probabilistic models (DDPM) are a class of generative models which have recently been shown to produce excellent samples. We show that with a few simple modifications, DDPMs can also achieve competitive log-likelihoods while maintaining
arxiv.org
DDPM을 먼저 보고 오면 이해하기 훨씬 쉬울겁니다.
Abstract
저자는 최근 DDPM이 excellent samples를 만들어냈지만 loglikelihood는 그다지 competitive하지 못해서 few simple modification으로 competitive loglikelihood에 도달한 Improved DDPM을 제안한다.
1. Introduction
기존 DDPM에서는 $L_{simple}$ objective를 사용했지만 본 논문에서 $L_{hybrid}$를 제안하고 better log-likelihood를 얻었다고 말한다. 또한 DDPM은 high quality samples를 얻기 위해 수 백~수 천 번의 step이 필요했지만 우린 50번만으로 speeding up해서 좋은 samples를 얻었다고 말한다.
2. Denoising Diffusion Probabilistic Models
짧은 리뷰
DDPM에서의 Forward Process는 아래와 같이 정의한다.

물론 우리가 Reverse Distribution $q(x_{t-1}|x_t)$를 안다면 쉽게 sampling할 수 있겠지만 $q(x_{t-1}|x_t)$는 전체 데이터 분포에 의존하기 때문에 q대신 p로 근사하여 아래와 같은 식을 사용하였다. (variance는 학습하지 않는다는 점 기억)

그리고 위의 equation 1의 Markovian 성질을 이용하여 아래와 같이 sampling을 진행할 수 있음. 여기서 기억해야 할 것은 noise variance로 $\beta_t$대신 $1-\overline{\alpha_t}$을 쓴다는 것.

DDPM의 또다른 특징은 $L_{simple}$을 사용한다는 점.

근데 여기서 variance인 $\sum_\theta(x_t, t)$는 학습시키지 않고 대신 $\sigma_t^2I$로 fix시킴. 그리고 저자는 $\sigma_t^2 = \beta_t$나 $\sigma_t^2 = \widetilde{\beta_t}$나 유사한 sample quality를 낸다고 얘기함.
3. Improving the Log-likelihood
3.1 Learning $\sum_\theta(x_t, t)$

Figure 1을 보면 $\beta_t$와 $\widetilde{\beta_t}$가 t=0 근처일 때를 제외하고는 서로 가까워지며 유사한 결과를 내는 것을 확인할 수 있음. 즉, steps를 무한하게 두면 $\sigma_t$는 sample quality에 중요하지 않다는 것임.
=> diffusion steps를 늘릴수록, 분산보다 모델의 평균 $\mu_\theta(x_t, t)$가 $\sum_\theta(x_t, t)$보다 더 많이 분포를 결정한다고 볼 수 있음.
Figure 2는 diffusion process의 초기 few steps가 vlb의 대부분에 기여한다는 것을 확인할 수 있음. 따라서 저자는 $\sum_\theta(x_t, t)$를 잘 선택하면 log-likelihood를 잘 향상시킬 수 있을 거라고 말함. 이를 달성하기 위해, 저자는 DDPM에서 학습시키지 않는 $\sum_\theta(x_t, t)$를 학습시켜야 한다고 주장함.
본 논문에서는 $\sum_\theta(x_t, t)$를 직접 학습 시키지 않고 아래와 같이 $\beta_t$와 $\widetilde{\beta_t}$ 사이의 interpolation값으로 분산은 parameterize시켜서 사용함. (이 방법이 더 낫다고 말함)
모델의 output은 차원당 하나의 component를 포함하고 있는 vector v인데 이걸 분산으로 변환함

$L_{simple}$이 $\sum_\theta(x_t, t)$에 의존하지 않으므로 아래와 같이 term을 추가해줌.

실험을 통해 $\lambda=0.001$로 설정하였고 $L_{vlb}$ term안의 $\mu_\theta(x_t, t)$는 stop-gradient로 설정함.
why? => 이미 $L_{simple}$에서 $\mu_\theta(x_t, t)$를 학습하니까 $L_{vlb}$는 variance 학습에만 집중하게 만들기 위함.
3.2 Improving the Noise Schedule
아래 표와 같이 DDPM의 noise schedule은 linear해서 forward process 마지막 부분엔 too noisy해짐. 그래서 sample quality에 그다지 많은 기여를 하지 않음.
이 문제를 해결하기 위해, 저자는 $\overline{\alpha_t}$ term을 이용해 noise schedule를 다시 만들었음.

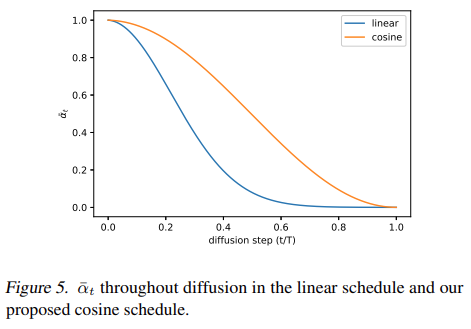
Figure 5에서 $\overline{\alpha_t}$의 cosine schdule은 완만하게 하강하는 것을 확인할 수 있으며 linear schdule은 0에 빠르게 도달하기 때문에 비교적 정보 파괴가 빠르게 이어짐.
t=0 근처일 때 $\beta_t$가 너무 작아지지 않도록 small offset s = 0.008로 설정해서 사용. $\beta_t$가 너무 작으면 $\epsilon$ 학습이 어려워져서 $\cos^2$를 사용했다고 함. 저자는 $\cos^2$이 common mathematical function이기에 임의로 설정하였다고 함.
3.3 Reducing Gradient Noise
저자는 $L_{hybrid}$를 optimizing하는 것보다 $L_{vlb}$를 optimizing하면 best log-likelihood가 나올거라 예상했지만 결과가 오히려 더 별로라서 놀랐다고 함. 따라서 이 점을 개선하기 위해 1가지 가설을 세움.
hypothesis : $L_{vlb}$는 $L_{hybrid}$보다 much noisier하기에 samplt t는 $L_{vlb}$에서 불필요한 noise를 uniform하게 유발
그리고 이 문제를 다루기 위해 아래와 같은 importance sampling을 함.

$E[L_t^2]$는 알려지지 않았고 학습 중 변경될 수 있는 값이라 각 loss term의 이전 10개 값들을 저장해두고 이를 update함.
학습초기에는? => 모든 t에 대해 uniformly 10개의 t를 sampling
위와 같은 방식으로 $L_{vlb}$를 optimizing하면서 best log-likelihood에 도달하였고 original한 $L_{vlb}$보다 noise를 상당히 줄임.
근데 위와 같은 방식으로 $L_{hybrid}$를 optmizing하면 그다지 도움이 되지 않는다고 함.
3.4 Results and Ablations
본 섹션에서는 위에서 얘기했던 best log-likelihood를 제거하고 $L_{vlb}$와 $L_{hybrid}$만 가지고 비교를 함.

4. Improving Sampling Speed
저자가 학습했던 모든 모델들의 diffusion steps는 4000이며 single sample을 만들어내려면 꽤 걸린다고 함. 그래서 Improving speed (performance 향상)을 위해 $L_{hybrid}$ 모델을 pre-trained시키는 방법을 제안하며 이 방법을 사용하면 적은 steps에도 high-quality samples를 만든다고 함. (without any fine-tuning)
T steps로 학습된 모델이 있을 때, 일반적으로 (1,2,...,T)로 이루어진 t values의 sequence로 sampling을 할 수 있는데, 이렇게 말고 임의로 t의 subsequence S를 사용해서 sampling하는 것도 가능함.
noise schedule $\overline{\alpha_t}$가 주어지면 S로 $\overline{\alpha}_{S_t}$를 구할 수 있고 아래와 같이 variance까지 얻을 수 있기 때문

위 방법으로 $\sum_\theta(x_{S_t}, S_t)$는 $\beta_{S_t}$와 $\widetilde{\beta_{S_t}}$ 사이로 parameterized되고 shorter diffusion process를 갖도록 rescaled될 수 있음. 따라서 우린 $p(x_{S_{t-1}}|x_{S_t)}$를 계산할 수 있게 됨.
아래 그래프를 보면 본 논문에서 제시한 방법 이외에 DDPM, DDIM이 있는데 ours가 가장 적은 steps에 낮은 FID를 달성했음을 확인할 수 있다.

저자는 100 steps만으로도 최적의 FID를 달성했다고 말한다.
1가지 흥미로운 점은 DDIM이 학습 초반에는 결과가 안좋지만 끝으로 갈수록 점점 좋아진다는 점을 확인할 수 있다.
5. Comparison to GANs
GAN과 비교하기 위해 precision, recall metric을 사용.
아래 Table 4를 보면 BigGAN-deep은 small model보다 FID가 월등히 높았지만 Recall부분에서는 낮게 나왔으므로 이 점을 미루어보아 diffusion models가 mode-coverage부분에서 GAN보다 더 좋다고 평가하였다.

6. Scaling Model Size
저자는 trend in modern ML은 larger models & more training time은 improve model performance로 이어진다며 layer수를 변경해가며 실험 결과를 확인하였다. 실험 모델은 $L_{hybrid}$를 ImageNet 64*64에서 각기 다른 4가지 모델을 실험하였으며 결과는 저자가 말했던대로 model capacity가 높아질수록 FID, NLL이 좋아진 것을 확인할 수 있다.

다만 위 결과는 $L_{vlb}$가 아니라 $L_{hybrid}$를 학습시킨 결과이므로 optimal log-likelihood는 아니라고 말한다.
7. Conclusion
종합해보면 Improved DDPM은 더 빠른 sampling을 하고 더 좋은 log-likelihood를 달성했다.
log-likelihood는 variance $\sum_\theta$를 학습시키면서 향상되었고 fewer steps만으로 sampling이 가능하다는 것을 보여주었다. 그리고 GAN이랑 비교했을 때 더 나은 mode coverage를 가진다는 것도 실험 결과를 통해 확인하였다.
'Diffusion' 카테고리의 다른 글
| TACKLING THE GENERATIVE LEARNING TRILEMMA WITH DENOISING DIFFUSION GANS (0) | 2023.06.07 |
|---|---|
| AnoDDPM: Anomaly Detection with Denoising DiffusionProbabilistic Models using Simplex Noise (0) | 2023.05.02 |
| ILVR : Conditioning Method for Denoising Diffusion Probabilistic Models (0) | 2023.02.28 |
| Denoising Diffusion Probabilistic Models (0) | 2023.02.02 |
| Denoising Diffusion Implicit Models (0) | 2023.01.27 |



