Generating High Fidelity Data from Low-densirt Regions using Diffusion Models : [arxiv]
Vikash Sehwag, Caner Hazirbas, Albert Gordo, Firat Ozgenel, Cristian Canton Ferrer
Princeton University, Meta AI
1. Introduction
대부분의 image datasets은 sample density에서 long-tailed distribution을 띄고 있으며 low-density에서의 samples는 high-density의 samples보다 높은 entropy를 갖는다.
본 논문의 목표는 generative model을 통해 low-density neighborhoods에서 synthetic images를 생성하는 것이다.
아래의 이유로 Diffusion을 사용한다.
GAN : high fidelity, poor coverage
Autoregressive models : high coverage, poor fidelity
Diffusion : high fidelity, high coverage
본 논문의 key distribution은 다음과 같다.
- Low density neighborhoods에서 samples를 생성하는 diffusion models를 제안
- Three different metrics을 통해 제안 방법이 기존의 방법들과 비교했을 때 성공했음을 검증
- Sampling process가 low density regions에서 training samples가 기억되지 않은 상태로 novel samples를 생성했음을 확인
2. Low-density sampling from diffusion models
2.1.1 Identifying low-density regions on data manifold
저자는 Diffusion과 함께 의미있는 embeddings를 잘 학습시키기 위해 discriminative model을 사용한다.
Gaussian model을 사용하여 각 클래스의 embeddings를 모델링하고 클래스 레이블 $y_i$를 갖는 $x_i$의 log likelihood를 추정한다. negative log likelihood를 아래의 식으로 나타내며 Hardness score (H)로 표기한다.
H가 높을수록 low density를 갖고 낮을수록 high density를 갖는다. 아래 식은 다변량정규분포를 찾아보면 이해가 쉽다.

$\mu_y$와 $\Sigma_y$는 각각 sample mean과 sample covariance를 의미하고 k는 embedding space의 차원을 의미한다.
Low-density regions에서 샘플링하기 위해 diffusion이 높은 hardness score를 갖는 샘플을 생성하도록 유도한다. 위의 Hardness score를 활용하여 아래의 contrastive guiding loss를 최대화한다. (correct class이면 낮은 likelihood를 갖도록 하기 위해)
$\tau$는 temperatrue, C는 클래스 개수를 의미한다.

위의 loss식을 활용하여 샘플링 시 각 time step에서 생성된 sample의 log-likelihood를 최소화하여 low-density regions으로 guide한다.

$\nabla^*$은 normalized gradients, $\alpha$는 scailing hyperparameter이다.
2.1.2 Maintaining fidelity when minimizing likelihood
저자는 $\alpha$값이 작을 때 sampling process가 매우 성공적이었다고 말하지만 반대로 값이 큰 경우에는 guidance term이 Gaussian transition term을 압도하게 되면서 생성이 잘 안된다고 한다. 특히 low-density regions은 sample 수가 너무 적기 때문에 분포를 근사할 수 없기 때문에 더 문제이다.
이 문제를 해결하기 위해 sampling process에서 term을 하나 추가한다. 추가된 term은 binary discriminator인 hardnes score H'이며 synthetic과 real을 판별한다. sampling시 synthetic이 real에 더 가깝게 배치하도록 아래의 loss를 최대화한다. 아래 식에서 0과 1은 각각 synthetic과 real을 뜻한다. 모델이 추정한 분포가 실제 데이터의 분포일 가능성이 낮은 low-density regions에서는 아래의 식을 통해 diffusion이 실제 data manifold에 가까운 sample을 생성하도록 만든다.
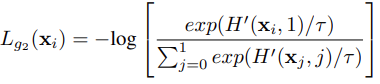
최종 샘플링 과정은 아래와 같다.


3. Experimental results
diffusion process T = 1000, sampling process step = 250
datasets : CIFAR-10, ImageNet
$\alpha$가 증가할수록 모델은 low-density regions에서 sampling을 유도하며, $\beta$는 real data manifold에 가깝게 배치되도록 한다.

3.1 Generating synthetic data using proposed $\alpha$-$\beta$ guided sampling process
저자가 제안한 sampling process에서 $\alpha$는 low-density regions으로부터 sampling되도록 하고 $\beta$는 생성된 이미지의 fidelity를 향상시키는 역할을 한다.
본 실험의 첫 번째 목표는 두 hyperparameters의 효과를 검증하는 것이다.
먼저 $\beta$가 0이고 $\alpha$를 0부터 1까지 증가시켰을 때의 결과(sampling된 이미지의 hardness score)가 (a)에 나타난다.
$\alpha$값이 커질수록 분포가 오른쪽으로 이동하는 것을 확인할 수 있다. 즉, lower estimated likelihood에서 높은 확률로 이미지를 sampling한다.
다음은 $\alpha$=0.5로 설정하고 $\beta$를 0부터 2까지 올렸을 때의 결과가 (b)에 나타난다. 값이 커질수록 synthetic image의 realism이 향상되는 것을 보여준다.

Comparing our sampling process with the baseline sampling process.
아래의 figure에서 baseline과 제안한 방법이 생성한 이미지를 비교한다.
top : proposed sampling approach
bottom : baseline sampling process

left : baseline sampling process
right : proposed sampling approach

3.2 Quantitative comparison of neighborhood density
제안한 sampling process가 low-density regions에서 생성되었다는 것을 확인하기 위해 다른 baseline들과 비교한다.
Metric은 다음과 같다.
Hardness score,
Average nearest neighbor(AVgkNN) : measures density using proximity to 5 nearest neighbors.
Local outlier factor(LOF) : improves on the nearest neighbor distance metric to compare density around a given sample to density around its neighbors.
높은 LOF값은 sample이 주변 neighbor보다 더 lower density region에 위치함을 의미한다.
Metric을 BigGAN, Real images from the ImageNet validation set, DDPM, proposed approach 4가지로 비교한다.
실험 결과는 아래와 같다. 제안한 방법이 low-density neighborhoods에서 높은 확률로 sample을 생성한 것을 확인할 수 있다.

Equivalent reduction in computational cost.
본 논문은 low-density neighborhoods에서 sample하기를 원한다. 달리 말하면 생성된 sample의 hardness score는 threshold보다 높아야 한다. naive한 rejection sampling approach는 기준에 만족하지 않는 sample들을 버린다. 이 점은 특히 low-density regions에서 잘 나타나며 계속 반복되는 sampling process에서 diffusion model은 computationally expensive하다.
따라서 rejection sampling은 계산 비용이 매우 높은 작업이다. 하지만 제안한 방법은 rejection sampling과 상관없으며 이 점은 아래의 실험 결과로 증명한다. 각 항목은 해당 score 범위 내에서 5K 256*256의 이미지를 생성하는 데 걸리는 일을 나타낸다.

4. Is our sampling process generating memorized sample from training data?
low-density regions은 제한된 sample 수만 이용 가능하기 때문에 생성 모델은 sample들을 기억할 수 있고 이 범위 내에서 novel sample을 만들지못할 수도 있다. 따라서 제안한 방법이 기억을 하는지 못하는지에 대해 검증한다.
Analyzing nearest-neighbor distance.
만약 training data가 기억되었다면 생성된 이미지는 실제 training data와 매우 유사할 것이다. 저자는 euclidean distance로 유사도를 구해서 잘 생성되었는지 확인한다. 만약 생성된 이미지가 training data로부터 기억이 되었다면 nearest-neighbor distance는 매우 작을 것이다.
validation set 내에 있는 real data와 nearest-neighbor distance를 측정한 결과이다. 결과를 통해 이미지들은 shape, texture , identity 등은 공유하지만 이런 속성들이 기억되지는 않는 것을 확인할 수 있다. 즉 diffusion이 sample을 기억하는 대신 data manifold를 학습했다는 것을 알 수 있다.
left : synthetic
right : real

Novel samples from low-density regions.
아래의 실험은 각 synthetic image와 real data내에서 synthetic과 가장 가까운 5개의 neighbor를 뽑아낸 결과이다.
synthetic의 nearest neighbor가 다른 label을 가지고 있는 경우도 나타나는데 이는 이 영역 내 training sample이 부족하기 때문이다. 그럼에도 real data내의 똑같은 label을 가진 image와는 많이 다른 것을 확인할 수 있다.
left : synthetic label
right : real label

5. Limitations and borader impact
저자는 본 논문을 통해 low-density regions에서 sampling process를 guide하는 방법을 제안했고 실험을 통해 diffusion model이 training data를 기억하지 않고 novel image를 만들었다.
저자는 ImageNet에서 어떤 memorization도 발견해지 못했지만 보다 더 복잡한 데이터셋에서는 기억하는 문제가 발생할 수도 있다고 한다.



